Bisher war der Ausgangspunkt der Minimierungssuche das Finden einer Geraden, sprich lineare Regression. Aber bei unserem Neuronalen Netzwerk geht es um Gewichte und Fehlerminimierung. Daher wird jetzt das Gradientenabstiegsverfahren noch einmal anhand von Gewichtsveränderungen erläutert. Das einfachste Beispiel hat nur ein Gewicht (s. Abbildung 34).

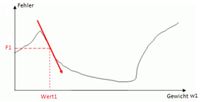
Abbildung 34 (*Q30): Gradient (Steigung) an dem Punkt P(Wert1, F1)

Auch hier kennt das Neuronale Netzwerk nicht die blaugrau eingezeichnete Fehler- bzw. Kostenfunktion. Sie weiß nur, dass der Gewichtswert Wert1 den Fehlerwert F1 verursacht. Also werden kurz vor und hinter dem Gewicht die beiden Fehlerwerte errechnet, damit die Steigung ermittelt und dann (bei negativer Steigung) in Richtung eines neuen (größeren) Gewichtswertes „gesprungen“ werden kann. Dies wird so oft gemacht, bis die Steigung gleich Null ist. Ein Minimum ist gefunden. Unter “http://www.neuronalesnetz.de/backpropagation4.html“ findet sich eine sehr gute animierte Veranschaulichung.

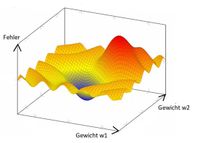
Abbildung 35 (*Q31): Gesamtfehler in Abhängigkeit von zwei Gewichten

Beim nächsten Beispiel gibt es schon 2 Gewichte und eine Fehler- bzw. Kostenebene mit lokalen Minima (s. Abbildung 35).

Der steilste Weg nach unten ist jetzt nicht in einer zweidimensionalen, sondern in einer dreidimensionalen Ebene. Auch dies ist noch gut zu verstehen. Aber in einem Neuronalen Netzwerk mit tausenden von Gewichten und somit zigtausenden Dimensionen hört die Vorstellungskraft auf. Nichtsdestotrotz schafft es die Mathematik für einen n-dimensionalen Punkt den Gradienten zu berechnen und über das Gradientenabstiegsverfahren ein Minimum zu finden. Dabei hängt das gefundene Minimum oft vom gewählten Startpunkt ab.

- 36 -