4.3. Lineare Regression und Gradientenabstiegsverfahren

Lineare Regression

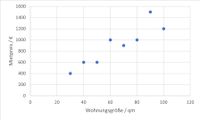
Die lineare Regression ist ein einfaches Verfahren des Maschinellen Lernens. Es wird versucht, für verschiedene gegebene Punkte (z. B. in einem zweidimensionalen Raum) eine Gerade so zu finden, dass die Gesamtsumme der einzelnen Abweichungen ein Minimum ist. Ein einfaches Beispiel (*Q29): Die Mietpreise y sind von der Größe x der Wohnungen abhängig (Abbildung 28 zeigt einige Trainingsdaten).

Abbildung 28 (*Q29): Reale Mietpreise für acht verschiedene Wohnungen

Wenn man einen linearen Zusammenhang vermutet, dann kann man nun die lineare Regression anwenden. Ziel soll es sein, dass man später für eine unbekannte Wohnung unter Berücksichtigung der Wohnungsgröße den Mietpreis vorhersagen kann. Dazu wird (wenn ein zweidimensionaler Raum vorliegt) eine Gerade gesucht, die möglichst nah an allen Punkten liegt. Die Gerade ist wie folgt definiert:

Mietpreis = m * Wohnungsgröße + b       mit   m = Δy / Δx

Kostenfunktion

Welche der vielen möglichen m-b-Kombinationen hat aber den geringsten Gesamtfehler? Hierfür wird erst einmal der Gesamtfehler als sog. Kostenfunktion definiert (s. Abbildung 29).

Abbildung 29 (*Q29): Kostenfunktion

- 32 -