3.1. Biologisches Neuron und künstliches Neuron (Perzeptron)

Ein vereinfachtes biologisches Neuronen-Modell zeigt Abbildung 11.

Abbildung 11 (*Q18): Biologisches Neuronen-Modell

Ein biologisches Neuron hat sehr viele Eingänge (Dendrite) und einen Ausgang (Axon), der aber aufgeteilt und mit vielen Eingängen anderer Neuronen verbunden werden kann (es gibt aber eigentlich nur ein y). Sind die ankommenden Signale von anderen Nervenzellen stark genug, wird ein bestimmter Schwellenwert der Erregung überschritten. Das Neuron sendet dann einen elektrischen Impuls über das Axon entlang in Richtung von Synapsen, die die Schnittstellen zu den nächsten Dendriten sind und meistens den elektrischen Impuls chemisch weitergeben.

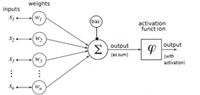
Es wurde versucht, dieses biologische Neuron mathematisch und informatisch abzubilden (s. Abbildung 12). Das Perzeptron (perceptron) ist ein von Frank Rosenblatt 1958 vorgestelltes vereinfachtes künstliches Neuronales Netz. Es besteht in der einfachsten Version aus genau einem künstlichen Neuron mit anpassbaren Gewichten und einem Schwellenwert (*Q15).

Abbildung 12 (*Q20): Prinzipieller Aufbau eines nachgebildeten Neurons (Perzeptrons)

Die Gewichte w1 bis wn schwächen oder stärken die jeweiligen Eingangssignale x1 bis xn. Danach werden alle gewichteten Eingangssignale aufaddiert. Zusätzlich gibt es einen sog. Bias-Wert (Bias-Term, Verzerrungswert, Schwellwert, Nullwert), der z. B. dafür sorgt, dass, wenn alle Eingänge Null sind, das Ausgangssignal nicht zwingend Null sein muss:

x1 * w1 + x2 * w2 + … + xn * wn + 1 * bias = output (as sum)

Die Multiplikation des Bias-Werts mit 1 soll andeuten, dass der Bias quasi auch ein Gewicht ist, welches immer den konstanten virtuellen Eingangswert 1 gewichtet.

Die Anzahl der Gewichte ist somit immer um eins höher (n+1) als die Anzahl der Eingangssignale (n).

- 10 -